水锤现象严重时,管道再好也扛不住!清除水锤现象快来看这篇!
发布时间:2020-04-30
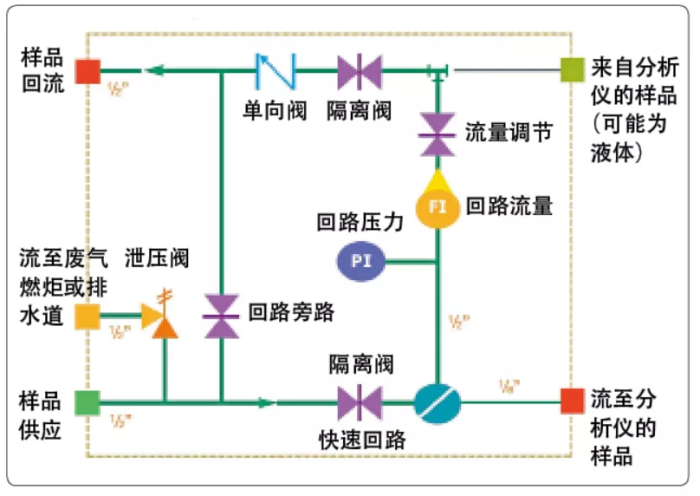
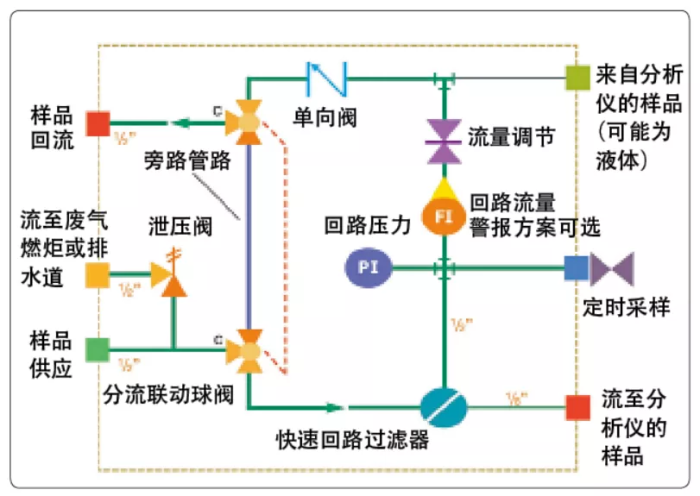
评估并尽量消除液体采集系统的水锤现象——水锤现象这一普遍但经常未能清理的故障会给所有液体采样系统带来重大威胁。水锤式敲击可能潜伏在系统当中,也可能随时破坏液体系统部件。

因此解决水锤问题的第一步是估算这种冲击现象给系统造成的压力尖峰值。我们可以采用儒可夫斯基方程来计算此值。这里取采样液体密度为p,此方程用于估算当液体流速u突然变化时,相对于压力脉动ΔP的水锤现象波幅:
ΔP = c·p·Δu,参数c为实际运行条件下液体内部声速。
例如,20℃时水内声速约为1 400 m/s。
因此,当阀门操作导致流速为1 m/s的水流突然断流时,计算得到的压力脉动值为:
ΔP = 1 400 m/s-1 000 kg/m3 - 1 m/s,ΔP = 1.4 MPa。
在上述例子中,结果为采样系统当中会出现1.4 MPa的额外压力,而运营方极有可能根本未对这一额外压力做出应对计划,系统也可能无法承受这一压力。如果系统流速高于1 m/s,则压力尖峰值会更高。
儒可夫斯基方程提供了一项理论尖峰压力值,但在实际条件下,尖峰压力可能没有这么高。只有在流速突然变化时,这种脉动才会形成作用力。下一步,精调计算过程可以在下列公式当中将这些实际条件纳入考虑(其L为液体管路的长度):
t≥(2-L)/c,如果上例当中的水管长度为100 m,
则:t≥(200/1 400)-s,t≥142 ms。
在本例当中,t代表压力波向上游传播并反射回至阀门所用的时间。只有在反射回来的压力波返回并碰到一个关闭阀门时,完整的压力脉冲波才会形成。而上述计算结果表明,如果该阀门关闭用时超过142 ms,则脉冲波压力将低于计算所得压力,水锤脉冲波值将减至最小。
《流程工业》4月刊内容精选↓(持续更新...)
✌阀门世界的重建!专业盘点流体管理创新技术!
✌泵监控系统维护保养工作行动指南!优化泵监控系统,本文说透了!
✌来自太阳的驱动力!有关未来生物燃料的思考!
扫描这个二维码,你将获得第一手杂志资讯











跟帖
查看更多跟帖 已显示全部跟帖